Fast & full featured optimization heuristics framework

: a Heuristic Optimization Framework

is an open-source full-featured evolutionary computation framework which main purpose is to help you write your own stochastic optimization algorithms, insanely fast.

It focus on the efficiency of the implementation of solvers, by providing:

  • a modular design for several types of paradigms,
  • the largest codebase of existing components,
  • tools for automated design and selection of algorithms,
  • a focus on speed and several parallelization options.

Quick start ⤒

Download

Download the latest stable release.

Or clone the latest version: git clone https://github.com/nojhan/paradiseo.git

Build

As is a development framework, you do not really need to install it on all your systems. Just put it somewhere on your development computer, compile it from here and indicate where to find it to your favorite build system.

is mainly developed for Linux, on which it is straightforward to install a C++ build chain. For example, on Ubuntu 18.04: sudo apt install g++-8 cmake make libeigen3-dev libopenmpi-dev doxygen graphviz libgnuplot-iostream-dev

use the CMake build system, so building it should be as simple as: mkdir build ; cd build ; cmake -DEDO=ON .. && make -j

For more details, see the building section.

Develop

To show you how does a code look, you will find here a minimal implementation of the popular CMA-ES algorithm.

The code is presented without comments, to keep it short, but it is yet full-featured, as you will see if you compile it within the build directory, with c++ cmaes.cpp -I../eo/src -I../edo/src -DWITH_EIGEN=1 -I/usr/include/eigen3 -std=c++17 -L./lib/ -leo -leoutils -les -o cmaes and run ./cmaes --help

1 #include <eo> 2 #include <edo> 3 #include <es.h> 4 #include <do/make_pop.h> 5 #include <do/make_run.h> 6 #include <do/make_continue.h> 7 #include <do/make_checkpoint.h> 8 9 using R = eoReal<eoMinimizingFitness>; 10 using CMA = edoNormalAdaptive<R>; 11 12 R::FitnessType sphere(const R& sol) { 13 double sum = 0; 14 for(auto x : sol) { sum += x * x; } 15 return sum; 16 } 17 18 int main(int argc, char** argv) { 19 eoParser parser(argc, argv); 20 eoState state; 21 22 size_t dim = parser.createParam<size_t>(10, 23 "dimension", "Dimension", 'd', 24 "Problem").value(); 25 26 size_t max_eval = parser.getORcreateParam<size_t>(100 * dim, 27 "maxEval", "Maximum number of evaluations", 'E', 28 "Stopping criterion").value(); 29 30 edoNormalAdaptive<R> gaussian(dim); 31 32 auto& obj_func = state.pack< eoEvalFuncPtr<R> >(sphere); 33 auto& eval = state.pack< eoEvalCounterThrowException<R> >(obj_func, max_eval); 34 auto& pop_eval = state.pack< eoPopLoopEval<R> >(eval); 35 36 auto& gen = state.pack< eoUniformGenerator<R::AtomType> >(-5, 5); 37 auto& init = state.pack< eoInitFixedLength<R> >(dim, gen); 38 auto& pop = do_make_pop(parser, state, init); 39 pop_eval(pop,pop); 40 41 auto& eo_continue = do_make_continue( parser, state, eval); 42 auto& pop_continue = do_make_checkpoint(parser, state, eval, eo_continue); 43 auto& best = state.pack< eoBestIndividualStat<R> >(); 44 pop_continue.add( best ); 45 auto& distrib_continue = state.pack< edoContAdaptiveFinite<CMA> >(); 46 47 auto& selector = state.pack< eoRankMuSelect<R> >(dim/2); 48 auto& estimator = state.pack< edoEstimatorNormalAdaptive<R> >(gaussian); 49 auto& bounder = state.pack< edoBounderRng<R> >(R(dim, -5), R(dim, 5), gen); 50 auto& sampler = state.pack< edoSamplerNormalAdaptive<R> >(bounder); 51 auto& replacor = state.pack< eoCommaReplacement<R> >(); 52 53 make_verbose(parser); 54 make_help(parser); 55 56 auto& algo = state.pack< edoAlgoAdaptive<CMA> >( 57 gaussian , pop_eval, selector, 58 estimator, sampler , replacor, 59 pop_continue, distrib_continue); 60 61 try { 62 algo(pop); 63 } catch (eoMaxEvalException& e) { 64 eo::log << eo::progress << "STOP" << std::endl; 65 } 66 67 std::cout << best.value() << std::endl; 68 return 0; 69 }

Get help

If you need immediate support or have any question, the best way to get answers is to send an email to paradiseo-help@lists.gforge.inria.fr. You can also consult the help archives, subscribe to our (low traffic) mailing-list or consult its archives.

Alternatively, you can join us on the official chatroom. You can try the online webchat app, or if you already use Element.io, you can directly connect to the #paradiseo:matrix.org multi-user chatroom with your favorite client.

Rationale ⤒

Black-box and Gray-box Optimization Problems

targets the development of solvers for mathematical optimization problems for which you cannot compute gradients. The classical use case is the automated design or configuration of some system which is simulated.

It supports mono-objective and multi-objective functions, partial evaluation, several generic way to represent solutions and have all the tools for using your own representation.

does not provides tools for modelling your problem, but makes it easy to find the best algorithm to solve it.

Metaheuristics / Evolutionary Algorithms

targets the design of metaheuristics solvers using computational intelligence methods, a subdomain of artificial intelligence.

It was originally designed for Evolutionary Algorithms, but rapidly evolved to provide abstractions for several "grammars" for other metaheuristics (or search heuristics, or whatever you call them). As of today, it provides: evolutionary algorithms (evolution strategies, genetic algorithms, etc.), particle swarm optimization, local searches (greedy search, simulated annealing, etc.), estimation of distribution algorithms (covariance-matrix adaptation, etc.).

Why choosing ?

Learning a full-featured framework like very often seems overkill. However, we would like to stress out that you may forget some points while jumping to this conclusion.

Full-featured

provides the largest mature codebase of state-of-the-art algorithms, and focuses on (automatically) find the most efficient solvers.

The most classical impediment to the use of is that you just want to check if your problem can actually be solved with heuristics. You feel that it would be a loss of time to learn complex stuff if it ends being useless.

However, you should keep in mind that:

  • Metaheuristics do seem very easy to implement in textbooks, but the state-of-the art versions of efficient algorithms can be a lot more complex.
  • It is usually easy to get something to actually run, but it is far more difficult to get an efficient solver.
  • Metaheuristics performances on a given problem are very sensitive to small variations in the parameter setting or the choice of some operators. Which render large experimental plans and algorithm selection compulsory to attain peak efficiency.

Fortunately, have the largest codebase of the market, hardened along 20 years of development of tens of solvers. Additionally, it provides the tools to rapidly search for the best combination of algorithms to solve your problem, even searching for this combination automatically.

Efficient

is the fastest framework on the market, which is a crucial feature for modern and robust approach to solver design and validation (especially on combinatorial problems).

Another classical criticism against is that C++ is hard and that a fast language is useless because speed is not a concern when your objective function is dominating all the runtime.

However, we argue that:

  • The numerical optimization community often sees objective functions as monolithic “black-box”, but in combinatorial opimization, it is very often the case that the objective function can be only partially evaluated on neighbor solutions, which allows for (tremendous) speed gains. The Paradiseo-mo module is architectured around that idea, a feature that is not so often found in other frameworks.
  • During the design phase of your solver, you will need to estimate its performance against synthetic benchmarks that are fast to compute. In that case, fast computation means fast design iterations. And it's even more true if you plan to use automated design to find the best solver for your problem.
  • Modern C++ makes use of the very same high-level abstractions you would find in more accepted languages like Python. Sure, the syntax is cumbersome, but you will not see it after a while, given that you will work at the algorithm level.
  • C++ provides full type checking and the largest set of tooling for any modern language, which are your first line of defense against long-term bugs. Sure, it sometimes gives you the impression that you fight against the compiler, but chasing subtle interface bugs across a complex Python code is even harder.

How fast is ?

As indicated in the previous section, this speed is crucially useful for algorithm design and algorithm selection.

You can expect that validating an algorithm implemented with will be up to 10 times faster than its (heavily optimized) Python counterpart.

To give an order of magnitude:

  • If you use the "official" vanilla implementation of CMA-ES in Python/Numpy solving the BBOB problem suite through the COCO plateform, running the whole benchmark will take approximately 10 minutes on a single Intel Core i5 @ 2.50GHz with a solid state disk.
  • The same experiment, running the implementation using the seamless binding to the IOHprofiler BBOB implementation, will take 1 minute.

Those measures are for a sequential execution, both implementation are able to run in parallel mode.

CMA-ES solves numeric problems with quadratic complexity regarding the number of dimensions. If you target simpler algorithms, they will be faster but one can expect a similar behaviour.

The pycma used for the comparison rely on numpy for the heavy parts of the computations. If you use a pure Python implementation, the difference will be far greater.

Features ⤒

Component-based Design

Designing an algorithm with consists in choosing what components (called operators) you want to use for your specific needs, just as building a structure with Lego blocks.

If you have a classical problem for which available code exists (for example if you have a black-box problem with real-valued variables), you will just choose operators to form an algorithm and connect it to your evaluation function (which computes the quality of a given solution).

Example of the operators "slots" for designing an Evolutionary Algorithm. The red "Evaluation" is where you plug your objective function, the yellow slots are the ones that depends on your choice of encoding (if you do not use generic ones). The green slots can be used by any algorithm. Tens of alternative operators may exists for each slot.

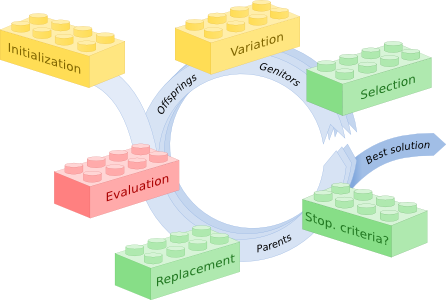
If your problem is a bit more exotic, you will have to code a class that encodes how solutions to your problem are represented, and perhaps a few more. For instance, you may want ad-hoc variations operators, but most of the other operators (selection, replacement, stopping criteria, command-line interface, etc.) are already available in .

One of the very powerful feature of is that its design targets easy combination of operators. Is is, for instance, straightforward to plug several different continuation operators in the stopping criterion slot of algorithms.

Popular combination of operators are provided as code-defined functions, with automatic command line argument control.

Additionally, this design allows for all kind of hybridizations between algorithms. For instance, it's easy to plug a local search algorithm as a variation operator of an evolutionary algorithm.

Another advantage is that you can very easily try alternative algorithms. With tens of operators available for popular slots, the number of different algorithms increase very rapidly. For instance, just using basic genetic algorithm operators with set parameters, can provide up to 5 millions different bitstrings algorithms. Given that metaheuristics are very sensitive to the interactions between operators, this approach allows for vital degrees of freedom.

Of course, it's also possible to add new algorithms "grammar". For instance, the grammar for estimation of distribution algorithms is an extension of the one for evolutionary algorithms. That way, you can re-use the operators already implemented for other algorithms.

The grammar of EDAs is extending the grammar of EAs, by adding an intermediate "distribution" data structure and operators manipulating it.

Large Choice of Components

is organized in several modules, either providing different "grammars" for different algorithms, either providing high-level features. All modules follows the same architecture design and are interoperable with the others, so that you can easily choose the subset of features you need.

The modules of .

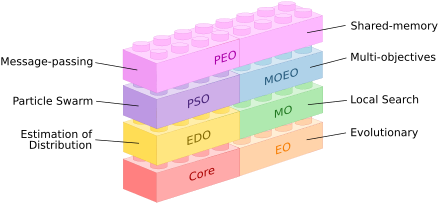
It is, for instance, easy to start with a simple local search, then add multi-objective capabilities, then shared-memory parallelization, then hybridization with an evolutionary algorithm and finally plug everything in an objective function so as to optimize the parameters with a particle swarm optimizer.

Below is an abridged list of components available in the EO module (only):

  • Flexible design that permits to easily create virtually any algorithm
  • Solution representation for continuous and combinatorial problems:
    • binary-strings,
    • permutations,
    • vectors,
    • easily write your own,
    • …
  • Several algorithm paradigms:
    • evolution strategies,
    • genetic algorithms,
    • estimation of distribution,
    • particle swarm optimization
    • …
  • Many selection and replacement operators:
    • rank-based,
    • deterministic or stochastic tournaments,
    • roulette,
    • elitism,
    • …
  • Ready-to-use variations operators:
    • uniform initializer,
    • gaussian mutation,
    • subtree crossover,
    • …
  • Easy combination of several operators:
    • proportional combination,
    • sequential call,
    • …
  • Parallelization tools:
    • Shared memory loops unrolling (with OpenMP)
    • Message passing parallelization (with openMPI):
      • map/reduce-like design, with operators choice, as in
      • useful existing operators (parallel dynamic multi-start, static evaluations, …)
  • Portable and human-readable parameter files
  • Suspend and load population from files
  • Versatile checkpointing and logging:
    • graphical display,
    • file dump,
    • various statistics,
    • signal catching,
    • …
  • Mersenne Twister random number generator (and various distributions)
  • No useless computation (sparing fitness call, functor-based calls)
  • And more!

Algorithm Selection and Configuration

provides meta-algorithmics features, like on-the-fly algorithm instanciation. This is useful to dynamically assemble and run an algorithm from a simple numerical encoding. This "algorithm forge" can handle a set of operators and parameter configurations, to be assembled in different "slots" to form an algorithm.

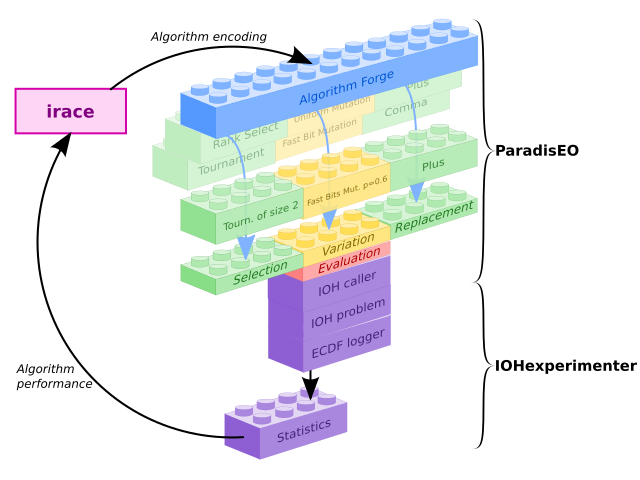
A simplified example of binding between , IOHexperimenter and irace. ParadisEO provides a on-the-fly algorithm instanciation, which is ran on an IOH problem, with performances estimated with a generic and fast module. All components figured with lego bricks forms a single, integrated, binary.

As the codebase provides generic algorithm and a large set of operators, it's easy to have access to a huge number of algorithms alternatives: there's easily millions of unique combinations.

To evaluate those algorithms, you can use bindings toward fast benchmarking tools (like IOHexperimenter), which allow for the fastests runs of the market.

You can then wrap this evaluation within an optimizer, to automatically search for the best algorithm instance. For instance, you can either use an optimizer made with , either plug the binary with irace ( provides an automatic interface generation) and reach budgets of 10 000 runs in just one hour (!).

And voilà! You started by just designing a high-level view of a solver, and you now know which algorithm instance allow for the best performance.

Note that the binding with IOHexperimenter also allow to easily import and explore experimental results in the IOHanalyzer HMI. Ohlala.

Portability

is mainly developed under Linux operating systems, where its dependencies and the C++ toolchain are easy to install. Recent versions have been tested with gcc and clang compilers.

Stable versions should however work on Windows and any Unix-like operating system with a standard-conforming C++ development system.

Previous versions of have been tested on the following platforms:

  • Linux x86 with GCC 3.x and 4.x
  • Linux x86_64 with GCC 3.x and GCC 4.x
  • MacOS X/Darwin PowerPC with GCC 3.x
  • MacOS X/Darwin x86 with GCC 4.x
  • Microsoft Windows using Cygwin's GCC 3.x (cygming special).
  • Microsoft Windows using Visual Studio 2003/2005; projects files are provided.
  • Solaris SPARC with GCC 3.x
  • Solaris x86 with GCC 3.x

Recent versions of uses the CMake portable build system, that permits to easily generate a build script for your environment.

If you have tested on a system not listed here, please let us know.

VS other Frameworks

The following tables show how compares to other active open-source frameworks, to the best of our knowledge (updated on 2019-10-18).

Projects
Framework Colored by speed level Language License If ‘Yes’, you have to disclose the sources of your solver when using this framework Copyleft Number of contributors Contrib. Number of lines of code ×1000 kloc
C++ LGPLv2/CeCill No 50 82
jMetal Java MIT No 29 60
ECJ Java AFLv3 Yes 33 54
OpenBeagle C++ LGPLv3 No 4 48
Jenetics Java Apachev2 No 10 47
ECF C++ MIT No 19 15
DEAP Python LGPLv3 No 45 9
Cllib Scala Apachev2 No 17 4
Features
Framework Evolutionary Algorithms EA Genetic Programming GP Estimation of Distribution Algorithms EDA Particle Swarm Opimization PSO Local Search LS Multi-Objective Optimization MO Parallelization for Clusters MPI Paralellization for Multicores MC Parallelization on GPU GPU Fitness Landscapes FL Algorithm Selection AS Score
Y Y Y Y Y Y Y Y N Y Y 10
ECJ Y Y Y N N Y Y Y Y N N 7
jMetal Y N N Y N Y Y N N N N 4
ECF Y Y N Y N N Y N N N N 4
DEAP Y N N N N Y Y Y N N N 4
OpenBeagle Y N N N N Y Y N N N N 3
Jenetics Y ? N N N Y N N N N N 2

Gathering and maintaining this information is not easy, so take them with a grain of salt, and if you see errors in those tables, please contact us.

Documentation ⤒

Academic Articles about

  • The latest state of the whole framework is introduced in the following article (see also the preprint):

    Johann Dreo, Arnaud Liefooghe, Sébastien Verel, Marc Schoenauer, Juan J. Merelo, Alexandre Quemy, Benjamin Bouvier, and Jan Gmys, Paradiseo: from a modular framework for evolutionary computation to the automated design of metaheuristics —22 years of Paradiseo—, GECCO'21: Proceedings of the Genetic and Evolutionary Computation Conference Companion, 1522–1530 (2021).

    If you used in a study, please cite the publication above:

    @inproceedings{Dreo-al_2021_Paradiseo,
        author    = {Dreo, Johann and Liefooghe, Arnaud and Verel, S\'{e}bastien and Schoenauer, Marc and Merelo, Juan J. and Quemy, Alexandre and Bouvier, Benjamin and Gmys, Jan},
        title     = {Paradiseo: From a Modular Framework for Evolutionary Computation to the Automated Design of Metaheuristics: 22 Years of Paradiseo},
        year      = {2021},
        isbn      = {9781450383516},
        publisher = {Association for Computing Machinery},
        address   = {New York, NY, USA},
        url       = {https://doi.org/10.1145/3449726.3463276},
        booktitle = {Proceedings of the Genetic and Evolutionary Computation Conference Companion},
        pages     = {1522–1530},
        numpages  = {9}
    }

  • The core EO module is described in the following scientific article:

    M. Keijzer, J.J. Merelo, G. Romero, G., M. Schoenauer, Evolving objects: A general purpose evolutionary computation library, Artificial Evolution, 2310, 829--888 (2002).

  • The multi-objective module (MOEO) is described in:

    A. Liefooghe, M. Basseur, L. Jourdan, E.-G. Talbi, -MOEO: A Framework for Evolutionary Multi-objective Optimization, EMO 2007, LNCS Vol. 4403, pp. 386-400, Matsushima, Japan.

  • The local search module (MO) is explained in:

    J. Humeau, A. Liefooghe, E-G. Talbi, S. Verel, -MO: From Fitness Landscape Analysis to Efficient Local Search Algorithms, Research Report RR-7871, INRIA, 2012.

  • A book about metaheuristics use as its framework of choice and explains in details several of its concepts, along with algorithmics content:

    El-Ghazali Talbi, Metaheuristics: from design to implementation, Wiley, 2009. (624pp), ISBN: 978-0-470-27858-1

Research Reports

Journal papers

Conference papers

  • A. Liefooghe, M. Basseur, L. Jourdan, E.-G. Talbi, "-MOEO: A Framework for Evolutionary Multi-objective Optimization", EMO 2007, LNCS Vol. 4403, pp. 386-400, Matsushima, Japan.
  • S. Cahon, N. Melab and E-G. Talbi, ": a framework for metaheuristics", International Workshop on Optimization Frameworks for Industrial Applications (ICOPI 2005), Paris, France, October 19-21, 2005.
  • S. Cahon, N. Melab and E-G. Talbi, "An Enabling Framework for Parallel Optimization on the Computational Grid", In Proceedings of the fifth IEEE/ACM International Symposium on Cluster Computing and the Grid (CCGRID'2005), Cardiff, UK, May, 2005.
  • S. Cahon, N. Melab, E-G. Talbi and M. Schoenauer, "PARADISEO based design of parallel and distributed evolutionary algorithms", Evolutionary Algorithms EA'2003, Marseille, France, LNCS, October 2003.


has been experimented on different academic and industrial problems. In this section, we present different applications that show the wide range of potential of this framework as it has been applied to scheduling problems, continuous optimization, data-mining applications, bioinformatic applications, telecommunication problem, etc.

Here is a list of some known publications that used :

Accelerator Physics

Bioinformatics

Metaheuristics Design

Automated Planning

Telecommunications

Cellular network design is a major issue in mobile telecommunication systems. A model of the problem in its full practical complexity, based on multiobjective constrained combinatorial optimization, has been investigated. We adopted the Pareto approach at resolution in order to compute a set of diversified non-dominated networks, thus removing the need for the designer to rank or weight objectives a priori.

Ref:

  • E-G. Talbi, S. Cahon and N. Melab. "Designing cellular networks using a parallel hybrid metaheuristic". Journal of Computer Communications, Elsevier Science, To appear in 2006.

Bi-objective flow-shop scheduling problem.

The flow-shop is one of the most widely investigated scheduling problem of the literature. But, the majority of studies considers it on a single-criterion form. However, other objectives than minimizing the makespan can be taken into account, like, e.g., minimizing the total tardiness.

Ref:

  • Arnaud Liefooghe, Matthieu Basseur, Laetitia Jourdan, El-Ghazali Talbi. "Combinatorial Optimization of Stochastic Multi-objective Problems: an Application to the Flow-shop Scheduling Problem". In S. Obayashi et al. (Eds.): Evolutionary Multi-Criterion Optimization (EMO 2007), LNCS vol. 4403, pp. 457-471, Matsushima, Japan (2007)

Electromagnetic properties of conducting polymer composites in the microwave band.

Due to the proliferation of electromagnetic interferences, designing protecting material for high frequencies equipments has become an important problem. A new multi-objective model is proposed to design the different layers of a conducting polymer. To solve this model, a multi-objective continuous genetic algorithm is used. This algorithm offers several solutions with different physical properties and different costs.

Ref:

  • Oliver Schuetze, Laetitia Jourdan, Thomas Legrand, El-Ghazali Talbi, Jean Luc Wojkiewicz, "A Multi-Objective Approach to the Design of Conducting Polymer Composites for Electromagnetic Shielding", EMO 2007, LNCS Vol. XX, pp. XX-XX, Matsushima, Japan.

Knowledge discovery in biological data from microarray experiments.

The problem of analyzing microarray data is actually a major issue in genomics. Often used techniques are clustering and classification. The authors propose to analyze those data through association rules. The problem is modeled as a multi-objective rule mining problem and a genetic algorithm is used to explore the large search space associated. Thence, MOGA permitted to present previously undiscovered knowledge.

Ref:

  • M. Khabzaoui, C. Dhaenens and E-G. Talbi, "A Cooperative Genetic Algorithm for Knowledge Discovery in MicroArray Experiments", In Parallel Computing for Bioinformatics and Computational Biology, Edited by Albert Y. Zomaya, ISBN: 0-471-71848-3, Chapter 13, pp 305-326, April 2006.
  • L. Jourdan, M. Khabzaoui, C. Dhaenens and E-G. Talbi, "A hybrid metaheuristic for knowledge discovery in microarray experiments", In Handbook of Bioinspired Algorithms and Applications, Edited by S. Olariu and A.Y. Zomaya, CRC Press, USA, ISBN: 1-58488-475-4, October 2005.

Molecular Docking and Protein Structure Prediction

Ref:

  • Alexandru-Adrian Tantar, Nouredine Melab, El-Ghazali Talbi, "A Comparative Study of Parallel Metaheuristics for Protein Structure Prediction on the Computational Grid", IEEE International Parallel & Distributed Processing Symposium(IPDPS 2007), pp. 1-10, 26-30 March 2007, Long Beach, California, USA.
  • A-A. Tantar, N. Melab, E-G. Talbi, O. Dragos and B. Parent, "A Parallel Hybrid Genetic Algorithm for Protein Structure Prediction on the Computational Grid", In Future Generation Computer Systems, Elsevier Science, vol. 23(3), pp. 398-409, 2007.
  • Alexandru-Adrian Tantar, Nouredine Melab, El-Ghazali Talbi and Bernard Toursel,"Solving the Protein Folding Problem with a Bicriterion Genetic Algorithm on the Grid", Fourth International Workshop on Biomedical Computations on the Grid(BioGrid'06), May 16-19, 2006, Singapore.

Protein identification.

Ref:

  • J-C Boisson, L. Jourdan, E-G. Talbi and C. Rolando "Protein Sequencing with an Adaptive Genetic Algorithm from Tandem Mass Spectrometry", CEC 2006, 0-7803-9489-5, July 16-21 2006, pp 1412-1419, Vancouver, Canada.
  • J-C. Boisson, L. Jourdan, E-G. Talbi and C. Rolando, "A Preliminary Work on Evolutionary Identification of Protein Variants and New Proteins on Grids", Second IEEE Workshop on High Performance Computing in Medicine and Biology (HiPComb 2006). Proccedings of the 20th International Conference on Advance Information Networking and Application, vol. 2, pp. 583-587. Vienne, Austria, April 18-20, 2006.

Engineering

Presentations Slides

The following documents aim to provide general overviews of the different 's modules. They are based on different pdf files which offer complementary view on both theoritical aspects and pratical use.

Paradiseo-EO

Paradiseo-MO

Paradiseo-MOEO

Tutorials

Examples on the differents metaheuristics are available in "tutorials" directory of each module of . Here you can find the corresponding explications.

Tutorials on EO (evolutionary algorithms module)

Tutorials on MO (local search module)

Tutorials on MOEO (multi-objective module)

  • MOEO Lesson1 Implement NSGA, NSGA-II and IBEA for the SCH1 problem
  • MOEO Lesson2 Evolutionary Algorithms for the flow-shop scheduling problem
  • MOEO Lesson3 Evolutionary Algorithms with a user-friendly parameter file
  • MOEO Lesson4 Dominance-based Local Search for the flow-shop scheduling problem

Tutorials SMP: new

  • SMP Lesson1 Algorithm wrapping with Master / Workers model

Tutorials on parallelization

Utilities

API documentation

The heart of is a set of classes implementing operators. Each module has a separate API documentation. If you want to browse the features and find which class to use, this is the right entry point

For your convenience, you can browse an online API doc for version 2.0:

Note that if you want to find the API documentation for the version you have at hand, just build the make doc target and open paradiseo/<build>/<module>/doc/html/index.html in your web browser.

Examples of real solvers

If you want to see examples of real solvers:

  • The examples page on INRIA pages (with explanations).
  • The contributed code on the project page.
  • The Descarwin project hold the "DaE" planning solver, which is implemented with and won the International Planning Competition.

Code ⤒

Downloads

The current stable release is version: Paradiseo 3.0.0-beta. Some other releases (older or newer) can be found on GitHub/paradiseo/releases.

You can obtain the latest stable and beta version directly via the Git repository: git clone https://github.com/jdreo/paradiseo.git. The release are on the "master" branch.

Or you can use (at your own risks) the development repositories of the developers:

Dependencies

In order to build the latest version of , you will need a C++ compiler supporting C++17. So far, GCC and CLANG gave good results under Linux. You will also need the CMake and make build tools.

A free working build chain under Windows seems always difficult to find. 2.0.1 was successfully tested with MinGW (minus the PEO module), but it's unsure if it still work for recent versions. If you managed to build under Windows, your feedback would be appreciated.

Some features are only available if some dependencies are installed:

  • Most of the EDO module depends on either uBlas or Eigen3. The recommended package is Eigen3, which enables the adaptive algorithms.
  • Doxygen is needed to build the API documentation, and you should also install graphviz if you want the class relationship diagrams.
  • GNUplot is needed to have the… GNUplot graphs at checkpoints.

To install all those dependencies at once under Ubuntu (18.04), just type: sudo apt install g++-8 cmake make libeigen3-dev libopenmpi-dev doxygen graphviz libgnuplot-iostream-dev.

Compilation

The build chain uses the classical workflow of CMake. The recommended method is to build in a specific, separated directory and call cmake .. from here. CMake will prepare the compilation script for your system of choice which you can change with the -G <generator-name> option (see the CMake doc for the list of available generators).

Under Linux, the default is make, and a build command is straitghtforward: mkdir build ; cd build ; cmake .. && make -j

There is, however, several build options which you may want to switch. To see them, we recommend the use of a CMake gui, like ccmake or cmake-gui. On the command line, you can see the available options with: cmake -LH ... Those options can be set with the -D<option>=<value> argument to cmake.

The first option to consider is CMAKE_BUILD_TYPE, which you most probably want to set to "Debug" (during development/tests) or "Release" (for production/validation).

Other important options are: EDO (which is false by default) and parallelization options: ENABLE_OPENMP, MPI, SMP.

By default, the build script will build the libraries only.

If you ENABLE_CMAKE_TESTING and BUILD_TESTING, it will be the tests, which you can run with the "ctest" command.

If you ENABLE_CMAKE_EXAMPLE, it will also build the examples.

Licenses

is distributed under the GNU Lesser General Public License and the CeCILL license (depending on the modules).

Note that those licenses places copyleft restrictions on a program created with , but does not apply these restrictions to other software that would links with the program.

Contribute

development is open and contributions are welcomed.

The official bug tracker is available on the project page.

If you have any question about contributing: subscribe to our (low traffic) mailing-list.

History ⤒

Authors

The EO module was started in 1999 by the Geneura Team at the University of Granada, headed by Juan Julián Merelo. The original Web site is also the only place where you will find old releases of (up to 0.8.7), but beware that it is not compatible at all with the current version.

You can read this PowerPoint presentation, that shows the EO philosophy back then. It includes a Visual Basic (!) macro for evolving objects in Visual Basic for Applications.

The developement team has then been reinforced by Maarten Keijzer, the C++ wizard who designed the current neat architecture), and Marc Schoenauer (who became a prominent researcher in the evolutionary algorithm community). Later came Jeroen Eggermont, who, among other things, did a lot of work on GP, INRIA Dolphin Team, Olivier König, who did a lot of useful additions and cleaning of the code and Jochen Küpper, working on infrastructure maintenance.

El-Ghazali Talbi's INRIA team did a lot of contributions starting from around 2003, on their own module collection called . Thomas Legrand, Sébastien Cahon and Nouredine Melab worked on parallelization modules. Arnaud Liefooghe worked a lot on the multi-objective module and on the local-search one along with Sébastien Verel and Jeremy Humeau. In the same team, C. C. and J. Boisson made significant contributions. Karima Boufaras specifically worked on (now deprecated) GPU tools.

The (then) EO project was then taken over by Johann Dreo, who worked with the help of Caner Candan on adding the EDO module. Johann and Benjamin Bouvier have also designed a MPI parallelization module. Alexandre Quemy also worked on parallelization codes.

In 2012, the two project (EO and ) were merged in a single one by Johann Dreo, Sébastien Verel and Arnaud Liefooghe, who act as maintainers ever since.

In 2020, automated algorithm selection tools and binding toward the IOH profiler validation tool were added.

Around 50 people contributed to so far and we cannot list them all, so thanks also to those not listed here.

Some softwares listed here are using , but they are not maintained by the team. They may not be free softwares.

  • DegaX is an ActiveX control which embeds 0.8.4.
  • EASEA was a GUI that permits to build evolutionary algorithm with or the GAlib. It is now a platform that allows program evolutionary algorithms on massively parallel many-core architectures.
  • GUIDE is a GUI that allows the generation of evolutionary algorithms. It can use or ECJ.